形式化大数数学 (0.0 - 高德纳箭头, 康威链箭)

交流Q群: 893531731
本文源码: Lower.lagda.md
高亮渲染: Lower.html

{-# OPTIONS --safe #-}
module Lower where
open import Relation.Binary.PropositionalEquality using (_≡_; refl)

本篇是形式化大数数学 (1.0 - 序数, 增长层级, 不动点)的前传, 我们快速介绍一些比较弱的著名大数记号, 这部分是入门的入门. 首先要理解的是各种大数记号的核心思想——迭代.

迭代

我们知道自然数类型 ℕ 由如下两条规则定义.

\frac{}{\kern{0.17em}\text{zero} : ℕ\kern{0.17em}} \qquad \frac{\alpha:ℕ}{\kern{0.17em}\text{suc}\kern{0.17em}\alpha:ℕ\kern{0.17em}}

open import Data.Nat using (ℕ; zero; suc)

约定我们用 A 表示任意类型.

private variable A : Set

定义函数 F : A → A 的 n 次复合叫做 F 的 n 次迭代, 记作 F^n

\begin{aligned} F^0 &= \text{id} \\ F^{n^+} &= F \circ F^n \end{aligned}

其中 \text{id} 是恒等函数, 就是输入什么返回什么.

open import Function public using (id; _∘_)

_∘ⁿ_ : (A → A) → ℕ → (A → A)
F ∘ⁿ zero  = id
F ∘ⁿ suc n = F ∘ (F ∘ⁿ n)

自然数算术

约定我们遵循类型论的习惯, 今后都会在无歧义的情况下省略函数应用的括号.

定义从 m 开始做 n 次后继叫做自然数加法, 记作 m+n

m + n := \text{suc}^n\kern{0.17em}m

_+_ : ℕ → ℕ → ℕ; infixl 6 _+_
m + n = (suc ∘ⁿ n) m

定义从 0 开始做 n 次 + m 叫做自然数乘法, 记作 m×n, 简记作 mn

m × n := (+m)^n\kern{0.17em}0

_*_ : ℕ → ℕ → ℕ; infixl 7 _*_
m * n = ((_+ m) ∘ⁿ n) 0

定义从 1 开始做 n 次 × m 叫做自然数幂运算, 也叫乘方, 记作 m^n

m^n := (×m)^n\kern{0.17em}1

_^_ : ℕ → ℕ → ℕ; infixr 8 _^_
m ^ n = ((_* m) ∘ⁿ n) 1

例

2^5 = 32 \\ 3^5 = 243

_ : 2 ^ 5 ≡ 32
_ = refl

_ : 3 ^ 5 ≡ 243
_ = refl

阿克曼函数

阿克曼函数 (Ackermann function) 是最简单和最早发现的非原始递归的可计算全函数. 它有很多版本, 常见的双参数版本定义如下.

定义双参数阿克曼函数 \text{Ack}\kern{0.17em}m\kern{0.17em}n

\begin{aligned} \text{Ack}\kern{0.17em}0 &:= \text{suc} \\ \text{Ack}\kern{0.17em}m^+\kern{0.17em}n&:= (\text{Ack}\kern{0.17em}m)^n\kern{0.17em}(\text{Ack}\kern{0.17em}m\kern{0.17em}1) \end{aligned}

Ack : ℕ → ℕ → ℕ
Ack zero = suc
Ack (suc m) n = (Ack m ∘ⁿ n) (Ack m 1)

数值表

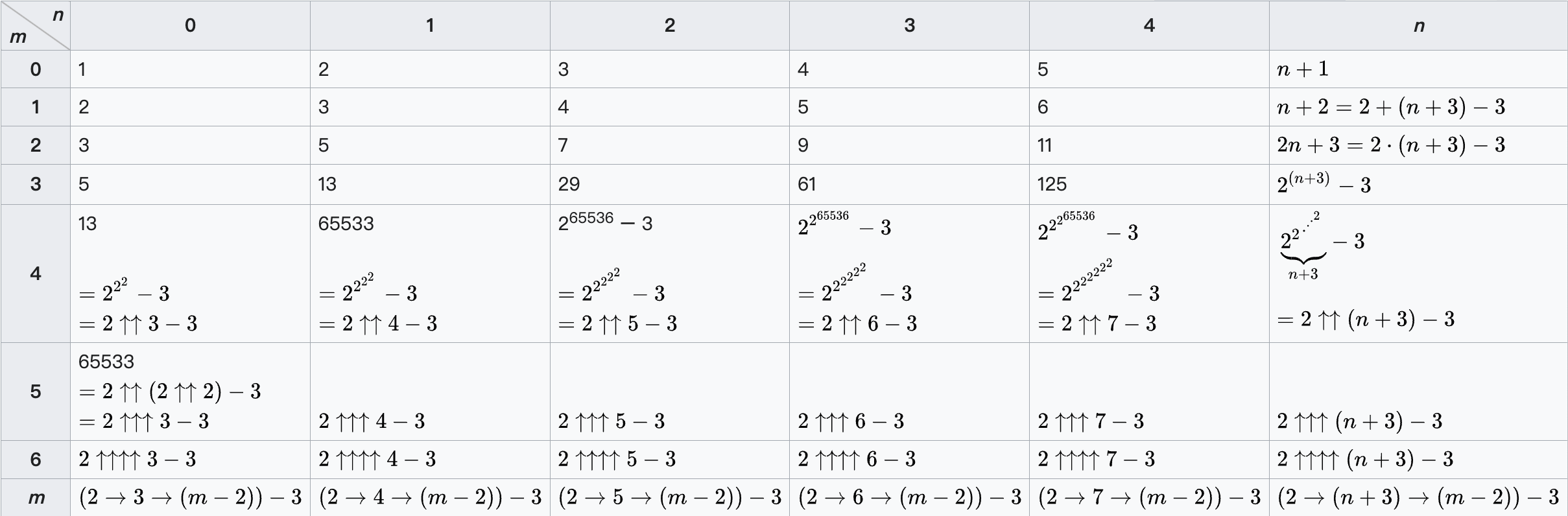
_ : Ack 0 4 ≡ 5
_ = refl

_ : Ack 1 4 ≡ 6
_ = refl

_ : Ack 2 4 ≡ 11
_ = refl

_ : Ack 3 4 ≡ 125
_ = refl

从表中第 n 列的形式可以看到 \text{Ack}\kern{0.17em}m 大致具有第 m 级运算的增长率. 其中的高德纳箭头 ↑ 和康威链箭 → 介绍如下.

高德纳箭头

高德纳箭头 (Knuth’s up-arrow notation) 是「将乘方看作乘法的迭代」这一思想的推广. 零个箭头是加法的迭代 (乘法), 一个箭头是乘法的迭代 (乘方), 两个箭头是一个箭头的迭代, 以此类推.

定义高德纳箭头有三个参数, 左右两边是底数和指数, 中间是箭头的数量.

\begin{aligned} m ↑^0 n &:= mn \\ m ↑^{k^+} 0 &:= 1 \\ m ↑^{k^+} n^+ &:= (m ↑^k)^n\kern{0.17em}m \end{aligned}

_↑⟨_⟩_ : ℕ → ℕ → ℕ → ℕ; infixr 9 _↑⟨_⟩_
m ↑⟨ zero ⟩ n = m * n
m ↑⟨ suc k ⟩ 0 = 1
m ↑⟨ suc k ⟩ suc n = ((m ↑⟨ k ⟩_) ∘ⁿ n) m

例

\begin{aligned} 2 ↑^0 3 &= 2×3 &=& 2 + 2 + 2 \\ 2 ↑^1 3 &= 2^3 &=& 2 × 2 × 2 \\ 2 ↑^2 3 &= {^3}2 &=& 2 ^ {2 ^ 2} \\ 2 ↑^3 3 &&=& 2 ↑^2 2 ↑^2 2 \end{aligned}

_ : 2 ↑⟨ 0 ⟩ 3 ≡ 2 + 2 + 2
_ = refl

_ : 2 ↑⟨ 1 ⟩ 3 ≡ 2 * 2 * 2
_ = refl

_ : 2 ↑⟨ 2 ⟩ 3 ≡ 2 ^ 2 ^ 2
_ = refl

_ : 2 ↑⟨ 3 ⟩ 3 ≡ 2 ↑⟨ 2 ⟩ 2 ↑⟨ 2 ⟩ 2
_ = refl

葛立恒数

葛立恒数 (Graham’s number) 是一个入门级别的著名大数, 直观上是一个64层的箭头塔.

定义定义辅助函数 G : ℕ → ℕ, 从4个箭头开始, 迭代 3 ↑^n 3 作为箭头数量, 即

\begin{aligned} G\kern{0.17em}0 &:= 4 \\ G\kern{0.17em}n^+ &:= 3 ↑^n 3 \end{aligned}

非形式地

G\kern{0.17em}n := 3 ↑^{3 ↑^{... ↑^{3 ↑↑↑↑ 3} ...} 3} 3

则葛立恒数为 G\kern{0.17em}64.

module Graham where
  G : ℕ → ℕ
  G zero = 4
  G (suc n) = 3 ↑⟨ n ⟩ 3

  G64 : ℕ
  G64 = G 64

康威链箭

约定我们用 n,a_1,a_2,a_3,a_4,b,c 表示任意给定的自然数. n^{++} 表示 n 的两次后继, n^{+++} 表示 n 的三次后继.

private variable n a₁ a₂ a₃ a₄ b c : ℕ
private pattern 2+ n = suc (suc n)
private pattern 3+ n = suc (suc (suc n))

康威链箭 (Conway chained arrow notation) 是自然数的长度大于等于 2 的有限序列. 由右箭头连接, 如

a → b → ... → c → d

但这里的右箭头无关紧要, 简洁起见我们形式化为参数个数大于等于 2 的多元函数 C_{n^{++}}, 其中 n 表示参数个数.

C_{n^{++}}\kern{0.17em}a\kern{0.17em}b\kern{0.17em}...\kern{0.17em}c\kern{0.17em}d

C_2 就定义为乘方
C_3 等价于 n 个高德纳箭头
C_4 大致相当于高德纳箭头塔
…

形式地

定义

\begin{aligned} C_2\kern{0.17em}b\kern{0.17em}c &:= b^c \\ \end{aligned}

C₂ : ℕ → ℕ → ℕ
C₂ = _^_

\begin{aligned} C_3\kern{0.17em}a\kern{0.17em}b^{++}\kern{0.17em}c^{++} &:= C_3\kern{0.17em}a\kern{0.17em}(C_3\kern{0.17em}a\kern{0.17em}b^{+}\kern{0.17em}c^{++})\kern{0.17em}c^{+} \\ C_3\kern{0.17em}a\kern{0.17em}b\kern{0.17em}1 &:= C_2\kern{0.17em}a\kern{0.17em}b \end{aligned}

其中第二行的 c = 0 的情况不存在, 因为 c = 1 时已退化为 C_2.

C₃ : ℕ → ℕ → ℕ → ℕ
C₃ a (2+ b) (2+ c) = C₃ a (C₃ a (suc b) (2+ c)) (suc c)
C₃ a b _ = C₂ a b

\begin{aligned} C_4\kern{0.17em}a_1\kern{0.17em}a_2\kern{0.17em}b^{++}\kern{0.17em}c^{++} &:= C_4\kern{0.17em}a_1\kern{0.17em}a_2\kern{0.17em}(C_4\kern{0.17em}a_1\kern{0.17em}a_2\kern{0.17em}b^{+}\kern{0.17em}c^{++})\kern{0.17em}c^{+} \\ C_4\kern{0.17em}a_1\kern{0.17em}a_2\kern{0.17em}b\kern{0.17em}1 &:= C_3\kern{0.17em}a_1\kern{0.17em}a_2\kern{0.17em}b \end{aligned}

C₄ : ℕ → ℕ → ℕ → ℕ → ℕ
C₄ a₁ a₂ (2+ b) (2+ c) = C₄ a₁ a₂ (C₄ a₁ a₂ (suc b) (2+ c)) (suc c)
C₄ a₁ a₂ b _ = C₃ a₁ a₂ b

\begin{aligned} C_5\kern{0.17em}a_1\kern{0.17em}a_2\kern{0.17em}a_3\kern{0.17em}b^{++}\kern{0.17em}c^{++} &:= C_5\kern{0.17em}a_1\kern{0.17em}a_2\kern{0.17em}a_3\kern{0.17em}(C_5\kern{0.17em}a_1\kern{0.17em}a_2\kern{0.17em}a_3\kern{0.17em}b^{+}\kern{0.17em}c^{++})\kern{0.17em}c^{+} \\ C_5\kern{0.17em}a_1\kern{0.17em}a_2\kern{0.17em}a_3\kern{0.17em}b\kern{0.17em}1 &:= C_4\kern{0.17em}a_1\kern{0.17em}a_2\kern{0.17em}a_3\kern{0.17em}b \end{aligned}

C₅ : ℕ → ℕ → ℕ → ℕ → ℕ → ℕ
C₅ a₁ a₂ a₃ (2+ b) (2+ c) = C₅ a₁ a₂ a₃ (C₅ a₁ a₂ a₃ (suc b) (2+ c)) (suc c)
C₅ a₁ a₂ a₃ b _ = C₄ a₁ a₂ a₃ b

现在我们要推广到任意 n \ge 2 元. 观察 C_2 到 C_5 的形式, 不难发现 C_2, C_3\kern{0.17em}a, C_4\kern{0.17em}a_1\kern{0.17em}a_2, C_5\kern{0.17em}a_1\kern{0.17em}a_2\kern{0.17em}a_3 的类型都是 ℕ → ℕ → ℕ, 于是可以抽象出以下共通形式

\begin{aligned} C_+ &: (ℕ → ℕ → ℕ) → ℕ → ℕ → ℕ → ℕ \\ C_+\kern{0.17em}C\kern{0.17em}a\kern{0.17em}b^{++}\kern{0.17em}c^{++} &:= C_+\kern{0.17em}C\kern{0.17em}a\kern{0.17em}(C_+\kern{0.17em}C\kern{0.17em}a\kern{0.17em}b^{+}\kern{0.17em}c^{++})\kern{0.17em}c^{+} \\ C_+\kern{0.17em}C\kern{0.17em}a\kern{0.17em}b\kern{0.17em}1 &:= C\kern{0.17em}a\kern{0.17em}b \end{aligned}

C₊ : (ℕ → ℕ → ℕ) → ℕ → ℕ → ℕ → ℕ
C₊ C a (2+ b) (2+ c) = C₊ C a (C₊ C a (suc b) (2+ c)) (suc c)
C₊ C a b _ = C a b

于是我们可以将 C_3 到 C_5 的定义换成

\begin{aligned} C_3 &:= C_+\kern{0.17em}C_2 \\ C_4\kern{0.17em}a &:= C_+\kern{0.17em}(C_3\kern{0.17em}a) \\ C_5\kern{0.17em}a_1\kern{0.17em}a_2 &:= C_+\kern{0.17em}(C_4\kern{0.17em}a_1\kern{0.17em}a_2) \end{aligned}

C₃′ : ℕ → ℕ → ℕ → ℕ
C₃′ = C₊ C₂

C₄′ : ℕ → ℕ → ℕ → ℕ → ℕ
C₄′ a = C₊ (C₃′ a)

C₅′ : ℕ → ℕ → ℕ → ℕ → ℕ → ℕ
C₅′ a₁ a₂ = C₊ (C₄′ a₁ a₂)

但现在我们还写不出任意 C_n, 因为首先要写出它的类型.

定义陪域为 A 的有限元自然数函数 \overbrace{ℕ→...→ℕ}^n →A, 记作 A^{→n}, 递归定义为

\begin{aligned} A^{→0} &:= A \\ A^{→n^+} &:= ℕ → A^{→n} \end{aligned}

_→ⁿ_ : Set → ℕ → Set
A →ⁿ zero = A
A →ⁿ suc n = ℕ → A →ⁿ n

观察 C_+ 的类型, 为了适用它, 还需要柯里化和反柯里化前 n 个参数. 我们使用自然数的 n 维向量 \vec{a}^n : \text{Vec}\kern{0.17em}ℕ\kern{0.17em}n 来容纳反柯里化出来的 n 个参数. 我们用 [\kern{0.17em}] 表示空向量, 用 a :: \vec{a}^n 表示向量的头尾.

open import Data.Vec using (Vec; _∷_; [])

定义递归定义函数 \text{uncurry}_2 将 ℕ^{→n^{++}} 反柯里化为 \text{Vec}\kern{0.17em}ℕ\kern{0.17em}n → ℕ → ℕ → ℕ

\begin{aligned} \text{uncurry}_2\kern{0.17em}F\kern{0.17em}[\kern{0.17em}] &:= F \\ \text{uncurry}_2\kern{0.17em}F\kern{0.17em}(a :: \vec{a}^n) &:= \text{uncurry}_2\kern{0.17em}(F\kern{0.17em}a)\kern{0.17em}\vec{a}^n \end{aligned}

uncurry₂ : ℕ →ⁿ 2+ n → (Vec ℕ n → ℕ → ℕ → ℕ)
uncurry₂ {n = zero} F [] = F
uncurry₂ {n = suc n} F (a ∷ a⃗) = uncurry₂ (F a) a⃗

定义递归定义函数 \text{curry}_3 将 \text{Vec}\kern{0.17em}ℕ\kern{0.17em}n → ℕ → ℕ → ℕ → ℕ 柯里化为 ℕ^{→n^{+++}}

\begin{aligned} \text{curry}_3\kern{0.17em}F &:= F\kern{0.17em}[\kern{0.17em}] \\ \text{curry}_3\kern{0.17em}F\kern{0.17em}a &:= \text{curry}_3\kern{0.17em}λ \vec{a}^n , F\kern{0.17em}(a :: \vec{a}^n) \end{aligned}

curry₃ : (Vec ℕ n → ℕ → ℕ → ℕ → ℕ) → ℕ →ⁿ 3+ n
curry₃ {n = zero} F = F []
curry₃ {n = suc n} F a = curry₃ λ a⃗ → F (a ∷ a⃗)

终于

定义递归定义任意 n \ge 2 元康威链箭 C_{n^{++}} : \prod_n ℕ^{→n^{++}}

\begin{aligned} C_2\kern{0.17em}m\kern{0.17em}n &:= m^n \\ C_{n^{+++}} &:= \text{curry}_3\kern{0.17em}λ \vec{a}^n , C_+\kern{0.17em}(\text{uncurry}_2\kern{0.17em}C_{n^{++}}\kern{0.17em}\vec{a}^n) \end{aligned}

C₂₊ₙ : ℕ →ⁿ 2+ n
C₂₊ₙ {n = 0} = _^_
C₂₊ₙ {n = suc n} = curry₃ λ a⃗ → C₊ (uncurry₂ C₂₊ₙ a⃗)

注意我们的这个定义并非最简, 而是综合考虑了

能循序渐进地理解定义
能通过 Agda 的自动停机检查

事实不难验证

\begin{aligned} C_2\kern{0.17em}b\kern{0.17em}c &= b ^ c \\ C_3\kern{0.17em}2\kern{0.17em}2\kern{0.17em}1 &= C_2\kern{0.17em}2\kern{0.17em}2 \\ C_4\kern{0.17em}2\kern{0.17em}2\kern{0.17em}1\kern{0.17em}9 &= C_2\kern{0.17em}2\kern{0.17em}2 \\ C_5\kern{0.17em}2\kern{0.17em}2\kern{0.17em}2\kern{0.17em}1\kern{0.17em}9 &= C_3\kern{0.17em}2\kern{0.17em}2\kern{0.17em}2 \\ C_6\kern{0.17em}a_1\kern{0.17em}a_2\kern{0.17em}a_3\kern{0.17em}a_4\kern{0.17em}b^{++}\kern{0.17em}c^{++} &= C_6\kern{0.17em}a_1\kern{0.17em}a_2\kern{0.17em}a_3\kern{0.17em}a_4\kern{0.17em}(C_6\kern{0.17em}a_1\kern{0.17em}a_2\kern{0.17em}a_3\kern{0.17em}a_4\kern{0.17em}b^{+}\kern{0.17em}c^{++})\kern{0.17em}c^{+} \end{aligned}

_ : C₂₊ₙ {0} b c ≡ b ^ c
_ = refl

_ : C₂₊ₙ {1} 2 2 1 ≡ C₂₊ₙ {0} 2 2
_ = refl

_ : C₂₊ₙ {2} 2 2 1 9 ≡ C₂₊ₙ {0} 2 2
_ = refl

_ : C₂₊ₙ {3} 2 2 2 1 9 ≡ C₂₊ₙ {1} 2 2 2
_ = refl

_ : C₂₊ₙ {4} a₁ a₂ a₃ a₄ (2+ b) (2+ c) ≡ C₂₊ₙ {4} a₁ a₂ a₃ a₄ (C₂₊ₙ {4} a₁ a₂ a₃ a₄ (suc b) (2+ c)) (suc c)
_ = refl

更高增长率的函数请看正篇形式化大数数学 (1.0 - 序数, 增长层级, 不动点), 那里的起点就远大于以上定义的所有函数.